การคำนวณไฟฟ้า
เราสร้างรายการสูตรการคำนวณทั่วไปบางอย่างที่คุณอาจใช้เมื่อเลือกโซลิดสเตตรีเลย์ (SSR) / โซลิดสเตตโมดูล (SSM) หรือการออกแบบวงจร
ข้อควรสนใจ: HUIMU Industrial (HUIMULTD) ไม่รับผิดชอบต่อข้อผิดพลาดในข้อมูลหรือในการทำงานที่ปลอดภัยและ / หรือการดำเนินงานที่น่าพอใจของอุปกรณ์ที่ออกแบบจากข้อมูลนี้
สูตรคำนวณพลังงานไฟฟ้า
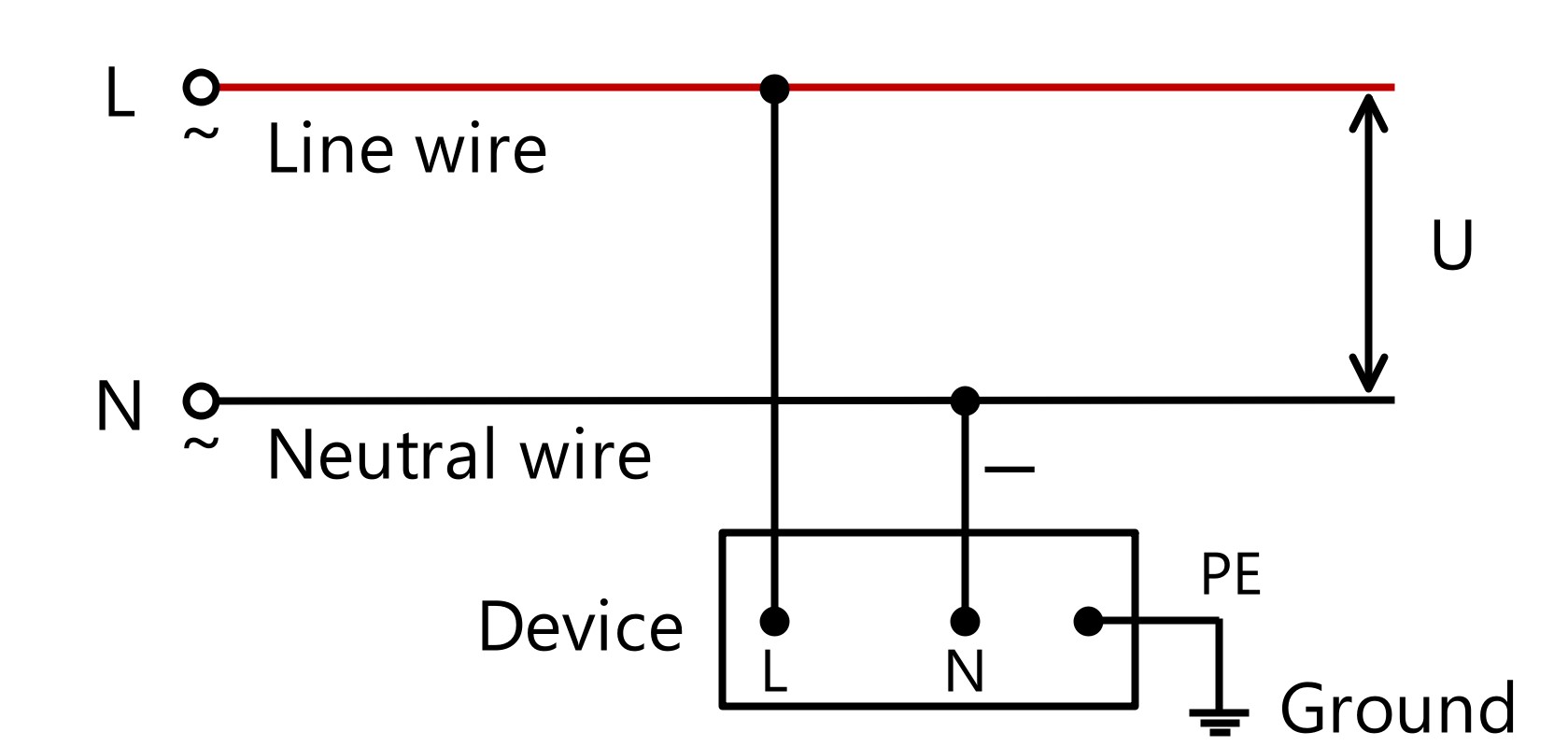
●โหลดเฟสเดียว
P = U · I ·cosφ
U คือแรงดัน (ปกติคือ 220VAC) ฉันเป็นกระแส
U คือแรงดัน (ปกติคือ 220VAC) ฉันเป็นกระแส
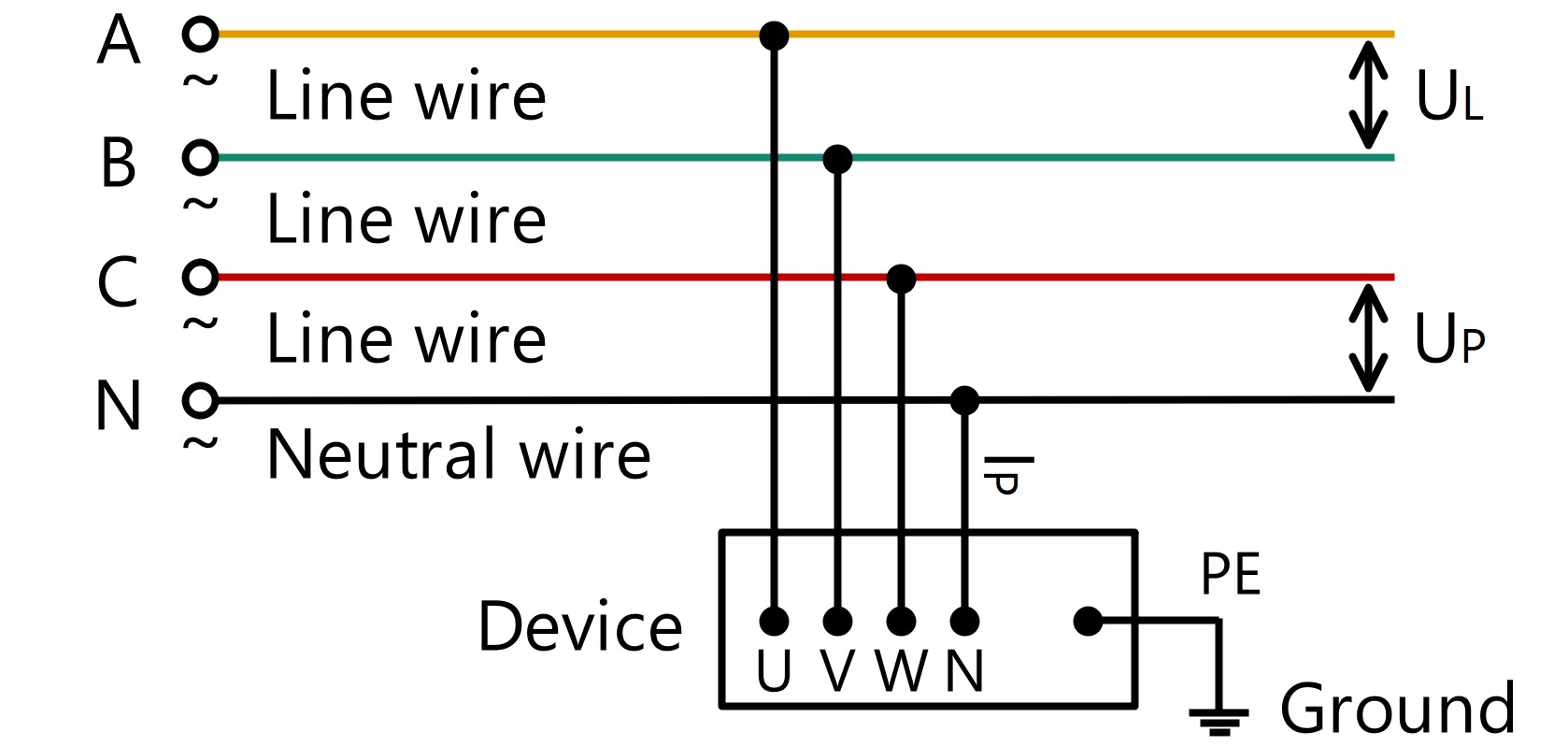
●โหลดสามเฟส
P = √3· U L · I L ·cosφ = 3 · U P · I P ·cosφ
U Lคือแรงดันสาย (ปกติ 380VAC), I Lคือกระแสไฟฟ้าในแนวตั้ง, U Pคือแรงดันเฟส (ปกติ 220VAC) , I Pคือเฟสปัจจุบัน
U Lคือแรงดันสาย (ปกติ 380VAC), I Lคือกระแสไฟฟ้าในแนวตั้ง, U Pคือแรงดันเฟส (ปกติ 220VAC) , I Pคือเฟสปัจจุบัน
● Power factor (cos φ)
หากประเภทโหลดเป็นโหลดตัวต้านทาน (เช่นฮีตเตอร์ไฟฟ้า) ดังนั้น cos φ = 1; หากประเภทโหลดเป็นโหลดแบบอุปนัย (เช่นมอเตอร์ไฟฟ้า) ดังนั้น 0 <cos φ <1 ยกตัวอย่างเช่นมอเตอร์ไฟฟ้าเมื่อมอเตอร์ไฟฟ้าเต็มแล้วกระแสไฟฟ้าที่ใช้งานมากที่สุดกระแสไฟฟ้าจะมีขนาดเล็กที่สุดและตัวประกอบกำลังอยู่ที่ 0.85 เมื่อโหลดมีน้ำหนักเบาหรือไม่มีโหลดกระแสไฟฟ้าที่ใช้งานอยู่จะมีขนาดเล็กกระแสไฟฟ้าที่เกิดปฏิกิริยาจะมีขนาดใหญ่และตัวประกอบกำลังอยู่ระหว่าง 0.4 และ 0.7 ดังนั้นเรามักจะใช้ตัวประกอบกำลัง 0.78 หรือ 0.8 หากประเภทโหลดเป็นโหลดแบบ capacitive (เช่นตัวชดเชยกำลังไฟฟ้า) ให้ระบุค่า cos φ <0
●มูลค่าสูงสุดมูลค่าที่มีประสิทธิภาพมูลค่าเฉลี่ย
แรงดันไฟฟ้ากระแสสลับเป็นคลื่นไซน์และค่าแรงดันไฟฟ้าจะเปลี่ยนเป็นระยะจาก 0 ถึงค่าสูงสุด (U MAX ) ดังนั้นค่าสูงสุด (U PK ) จึงเท่ากับค่าสูงสุด ค่าประสิทธิผล AC ถูกระบุโดยผลกระทบความร้อนของกระแสไฟฟ้านั่นคือปล่อยให้กระแส AC และกระแส DC ผ่านตัวต้านทานที่มีค่าความต้านทานเท่ากันตามลำดับและหากพวกเขาสร้างความร้อนเท่ากันในเวลาเดียวกันนั้นค่าที่มีประสิทธิภาพ ของกระแส AC นี้เท่ากับค่าของ DC current นี้ เนื่องจากค่าที่มีประสิทธิภาพของแรงดันไฟฟ้ากระแสสลับไซน์มีค่าเท่ากับรากของค่าเฉลี่ยกำลังสอง (U RMSหรือ U), U RMSโดยทั่วไปจะใช้เพื่อแสดงค่าที่มีประสิทธิภาพของแรงดันไฟฟ้ากระแสสลับ โดยปกติค่าแรงดันไฟฟ้า AC ที่เราตรวจพบผ่านอุปกรณ์ตรวจจับ (เช่นมัลติมิเตอร์) เป็นค่าแรงดันไฟฟ้าที่มีประสิทธิภาพและค่าแรงดันไฟฟ้า AC ที่ทำเครื่องหมายไว้บนอุปกรณ์ไฟฟ้าก็เป็นค่าที่มีประสิทธิภาพเช่น 220VAC, 380VAC แรงดันไฟฟ้า AC เฉลี่ย (U AV ) คือค่าแรงดันไฟฟ้าเฉลี่ยในช่วงเวลาหนึ่ง แรงดันไฟฟ้ากระแสสลับเฉลี่ยเท่ากับหนึ่งในแรงดันในหนึ่งรอบหารด้วย 2 cycle (เวลาในรอบเดียว) ในทางทฤษฎีค่าแรงดัน DC ที่ได้รับหลังจากการแก้ไขแบบเต็มคลื่นของแรงดันไฟฟ้า AC เท่ากับค่าเฉลี่ยของแรงดันไฟฟ้ากระแสสลับ
U PK = √2· U RMS = 1.414 · U RMS
U AV = 2 / π· U PK = 0.637 · U PK
U AV = 2 / π· U PK = 0.637 · U PK
ในทำนองเดียวกันตามกฎของ Ohm เราสามารถรับค่าสูงสุด (IPK หรือ IMAX) ค่าประสิทธิผล (IRMS) และค่าเฉลี่ย (IAV) ของกระแส AC
I PK = √2· I RMS = 1.414 · I RMS
I AV = 2 / π· I PK = 0.637 · I PK
I AV = 2 / π· I PK = 0.637 · I PK
เนื่องจากค่าของกระแส DC หรือแรงดัน DC เป็นค่าคงที่จึงไม่มีค่าสูงสุดค่าที่มีประสิทธิภาพและค่าเฉลี่ย
สูตรคำนวณปัจจัยการคำนวณ
เนื่องจากประสิทธิภาพของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตตนั้นได้รับผลกระทบจากสภาพแวดล้อมการทำงานและประเภทของโหลดจึงควรพิจารณา Derating Factor (หรือหลายปัจจัยปัจจุบัน) เมื่อเลือกค่าปัจจุบันของโซลิดสเตตรีเลย์ / โซลิดสเตตโมดูล .
I R = I L / α
I Rคือมูลค่าปัจจุบันของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตต
I Lคือค่ากระแสโหลด DC หรือค่าประสิทธิผลปัจจุบันของโหลด AC (ค่า rms);
αเป็นปัจจัยที่ทำให้เสื่อมเสีย
I Rคือมูลค่าปัจจุบันของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตต
I Lคือค่ากระแสโหลด DC หรือค่าประสิทธิผลปัจจุบันของโหลด AC (ค่า rms);
αเป็นปัจจัยที่ทำให้เสื่อมเสีย
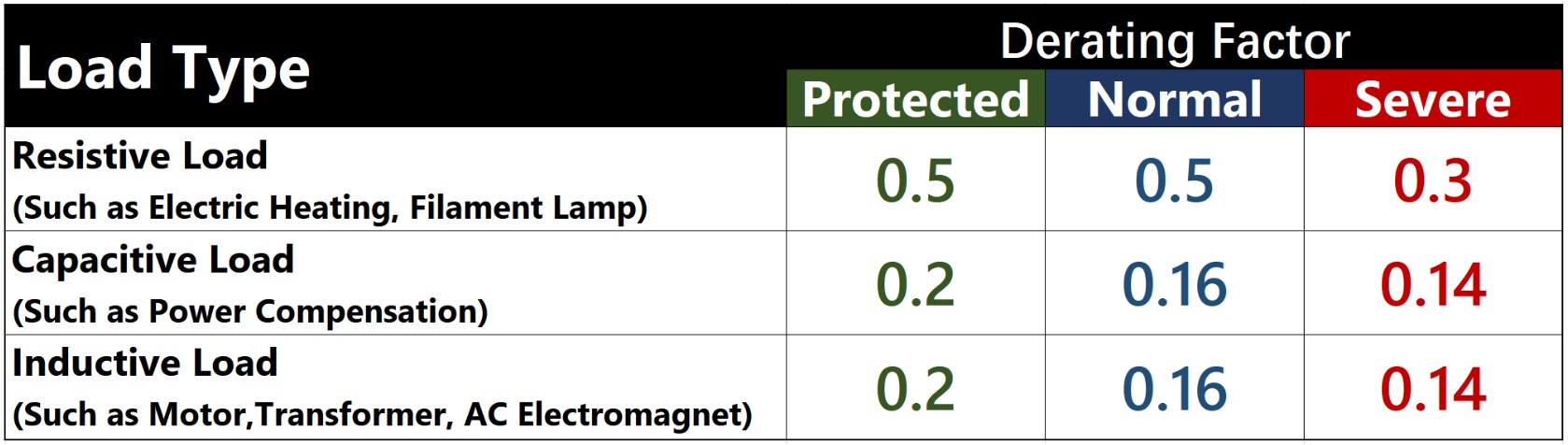
ตามสภาพแวดล้อมการทำงานของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตต (การระบายอากาศอุณหภูมิเวลาการให้บริการ ฯลฯ ) ปัจจัย Derating สามารถแบ่งออกเป็นสามระดับ: การป้องกันปกติและรุนแรง
สำหรับโหลดตัวต้านทาน (เช่นฮีตเตอร์ไฟฟ้าหลอดไฟ incandesc ent ฯลฯ ), α = 0.5 (ได้รับการป้องกัน), α = 0.5 (ปกติ), α = 0.3 (รุนแรง);
สำหรับโหลดอุปนัย (เช่นมอเตอร์หม้อแปลง ฯลฯ ), α = 0.2 (ได้รับการป้องกัน), α = 0.16 (ปกติ), α = 0.14 (รุนแรง);
สำหรับโหลดตัวเก็บประจุ (เช่นตัวชดเชยกำลังไฟฟ้า ฯลฯ ), α = 0.2 (ได้รับการป้องกัน), α = 0.16 (ปกติ), α = 0.14 (รุนแรง)
สำหรับโหลดตัวต้านทาน (เช่นฮีตเตอร์ไฟฟ้าหลอดไฟ incandesc ent ฯลฯ ), α = 0.5 (ได้รับการป้องกัน), α = 0.5 (ปกติ), α = 0.3 (รุนแรง);
สำหรับโหลดอุปนัย (เช่นมอเตอร์หม้อแปลง ฯลฯ ), α = 0.2 (ได้รับการป้องกัน), α = 0.16 (ปกติ), α = 0.14 (รุนแรง);
สำหรับโหลดตัวเก็บประจุ (เช่นตัวชดเชยกำลังไฟฟ้า ฯลฯ ), α = 0.2 (ได้รับการป้องกัน), α = 0.16 (ปกติ), α = 0.14 (รุนแรง)
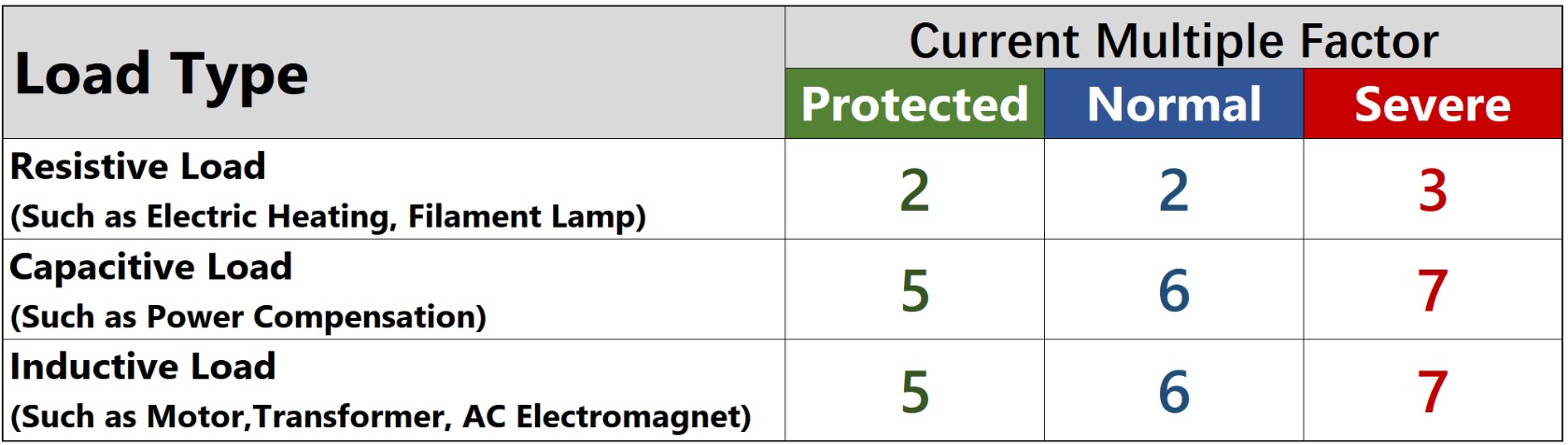
ปัจจุบันมีหลายปัจจัยที่ตรงกันข้ามกับ Derating Factor
I R = I L ·β
I Rคือมูลค่าปัจจุบันของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตต
I Lคือค่ากระแสโหลด DC หรือค่าประสิทธิผลปัจจุบันของโหลด AC (ค่า rms);
βเป็นปัจจัยหลายอย่างในปัจจุบัน
I Rคือมูลค่าปัจจุบันของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตต
I Lคือค่ากระแสโหลด DC หรือค่าประสิทธิผลปัจจุบันของโหลด AC (ค่า rms);
βเป็นปัจจัยหลายอย่างในปัจจุบัน
สำหรับโหลดตัวต้านทาน (เช่นฮีตเตอร์ไฟฟ้าหลอดไส้ ฯลฯ ), β = 2 (ได้รับการป้องกัน), β = 2 (ปกติ), (= 3 (รุนแรง);
สำหรับโหลดอุปนัย (เช่นมอเตอร์หม้อแปลง ฯลฯ ), β = 5 (ได้รับการป้องกัน), β = 6 (ปกติ), β = 7 (รุนแรง);
สำหรับโหลดตัวเก็บประจุ (เช่นตัวชดเชยกำลังไฟฟ้า ฯลฯ ), β = 5 (ได้รับการป้องกัน), β = 6 (ปกติ), β = 7 (รุนแรง)
สำหรับโหลดอุปนัย (เช่นมอเตอร์หม้อแปลง ฯลฯ ), β = 5 (ได้รับการป้องกัน), β = 6 (ปกติ), β = 7 (รุนแรง);
สำหรับโหลดตัวเก็บประจุ (เช่นตัวชดเชยกำลังไฟฟ้า ฯลฯ ), β = 5 (ได้รับการป้องกัน), β = 6 (ปกติ), β = 7 (รุนแรง)
ตัวอย่างเช่นถ้าคุณต้องการโซลิดสเตตรีเลย์แบบโซลิดสเตตเพื่อสลับ 220VAC, โหลดตัวต้านทาน 10A และต้องการโซลิดสเตตรีเลย์ในการทำงานอย่างต่อเนื่องในสภาพแวดล้อมการระบายอากาศที่ไม่ดีดังนั้นตามปัจจัย der = 3 (รุนแรง) คุณควรเลือก MGR-1D4830 (กระแสตรงเป็นไฟฟ้ากระแสสลับ, โหลด: 480VAC, 30A)
สูตรการคำนวณ Varistor
หากแรงดันไฟฟ้าสูงสุดของโหลดสูงให้แน่ใจว่าได้เชื่อมต่อวาริสเตอร์ (เช่น MOV, ZNR) พร้อมกับเทอร์มินัลเอาต์พุตของโซลิดสเตตรีเลย์ / โมดูลโซลิดสเตต
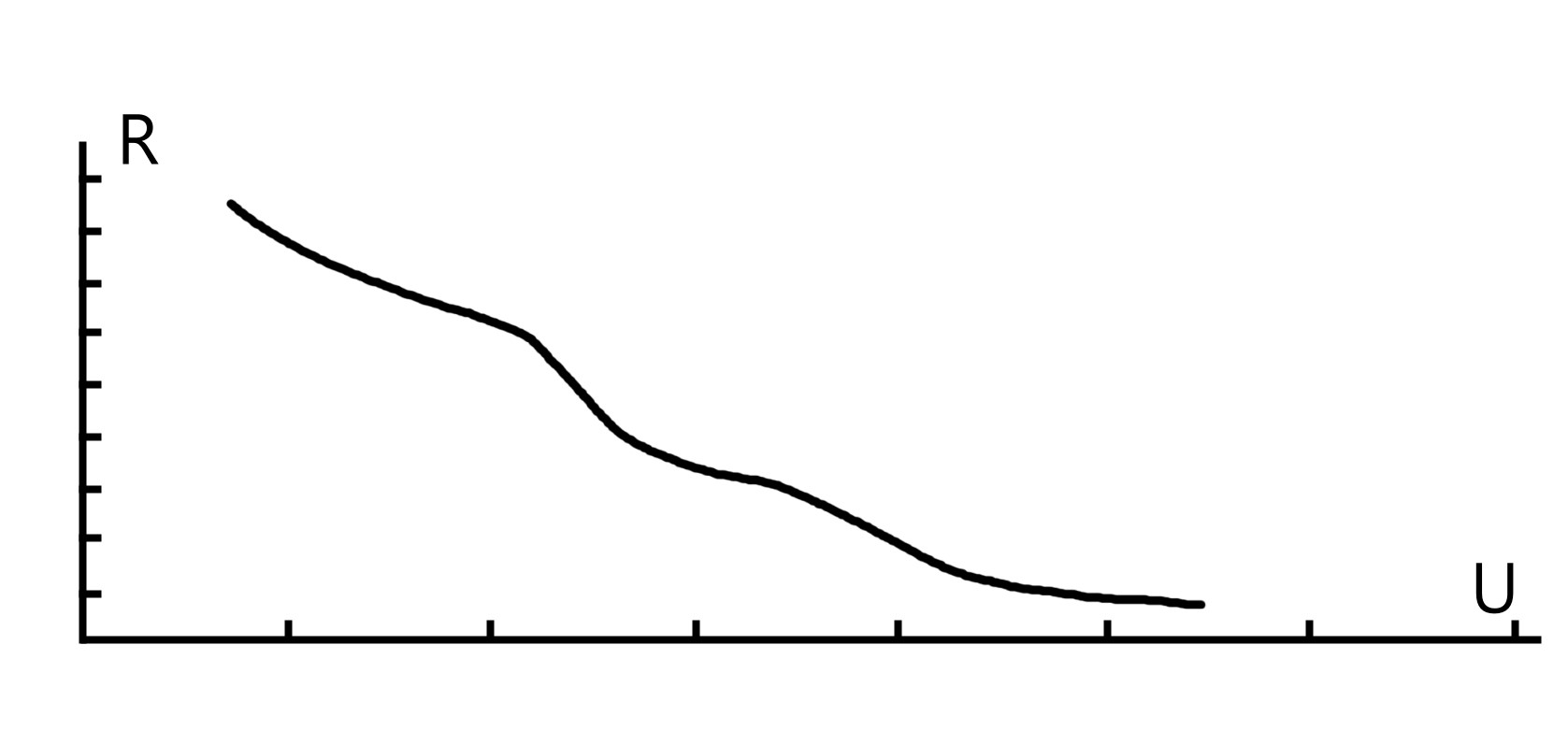
V imA = V 1mA = (a · v) / (b · c)
V imAคือแรงดันไฟฟ้าวาริสเตอร์เมื่อกระแสเป็น XmA เนื่องจากค่าปัจจุบันมักจะถูกตั้งค่าที่ 1mA ก็ยังสามารถแสดงเป็น V 1mA ; a คือค่าสัมประสิทธิ์ความผันผวนของแรงดันไฟฟ้าโดยทั่วไป 1.2; b คือค่าความผิดพลาดของวาริสเตอร์โดยทั่วไป 0.85; c คือสัมประสิทธิ์อายุของส่วนประกอบโดยทั่วไป 0.9; v คือแรงดันไฟฟ้า DC หรือแรงดันไฟฟ้า AC rms
V imAคือแรงดันไฟฟ้าวาริสเตอร์เมื่อกระแสเป็น XmA เนื่องจากค่าปัจจุบันมักจะถูกตั้งค่าที่ 1mA ก็ยังสามารถแสดงเป็น V 1mA ; a คือค่าสัมประสิทธิ์ความผันผวนของแรงดันไฟฟ้าโดยทั่วไป 1.2; b คือค่าความผิดพลาดของวาริสเตอร์โดยทั่วไป 0.85; c คือสัมประสิทธิ์อายุของส่วนประกอบโดยทั่วไป 0.9; v คือแรงดันไฟฟ้า DC หรือแรงดันไฟฟ้า AC rms
ดังนั้นสูตรข้างต้นสามารถทำให้ง่ายขึ้นเป็น:
สำหรับวงจร DC, V imA ≈1.6· v
สำหรับวงจร AC, V imA ≈1.6· V p = 1.6 ·√2· V AC
V pคือแรงดันไฟฟ้าสูงสุด, V ACเป็น คุณค่าที่มีประสิทธิภาพ
สำหรับวงจร DC, V imA ≈1.6· v
สำหรับวงจร AC, V imA ≈1.6· V p = 1.6 ·√2· V AC
V pคือแรงดันไฟฟ้าสูงสุด, V ACเป็น คุณค่าที่มีประสิทธิภาพ
โดยทั่วไปแรงดันไฟฟ้าวาริสเตอร์เป็น 1.6 เท่าแรงดันไฟฟ้าโหลด แต่เมื่อโหลดเป็นโหลดแบบอุปนัยแรงดันไฟฟ้าวาริสเตอร์ควร 1.6-1.9 เท่าแรงดันไฟฟ้าโหลดเพื่อความปลอดภัย
สูตรการคำนวณวงจรเรียงกระแส
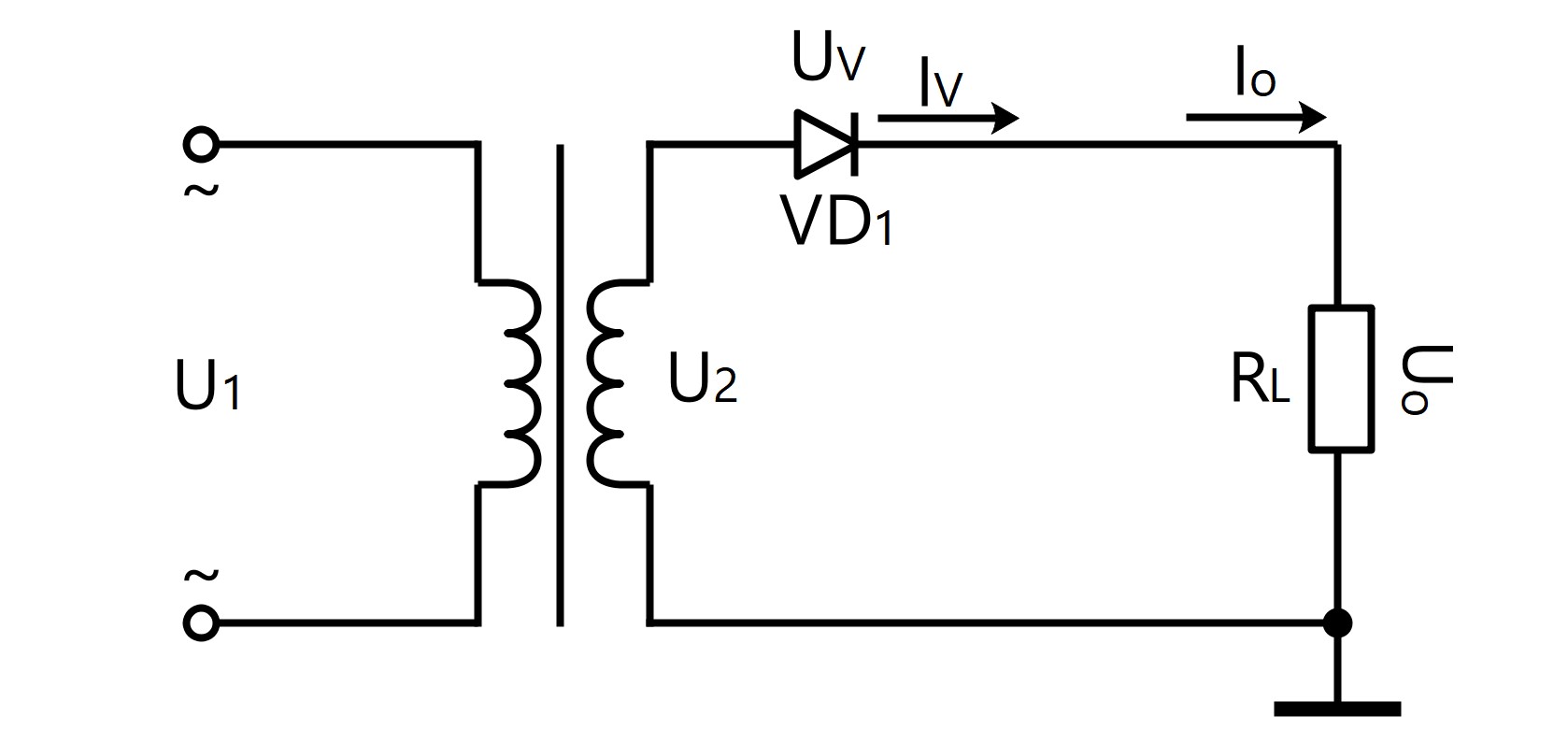
●วงจรการแก้ไขครึ่งคลื่นแบบเฟสเดียว
U 0 = 0.45 · U 2
I 0 = 0.45 · U 2 / R L
I V = I 0
U RM = √2· U 2
I 0 = 0.45 · U 2 / R L
I V = I 0
U RM = √2· U 2
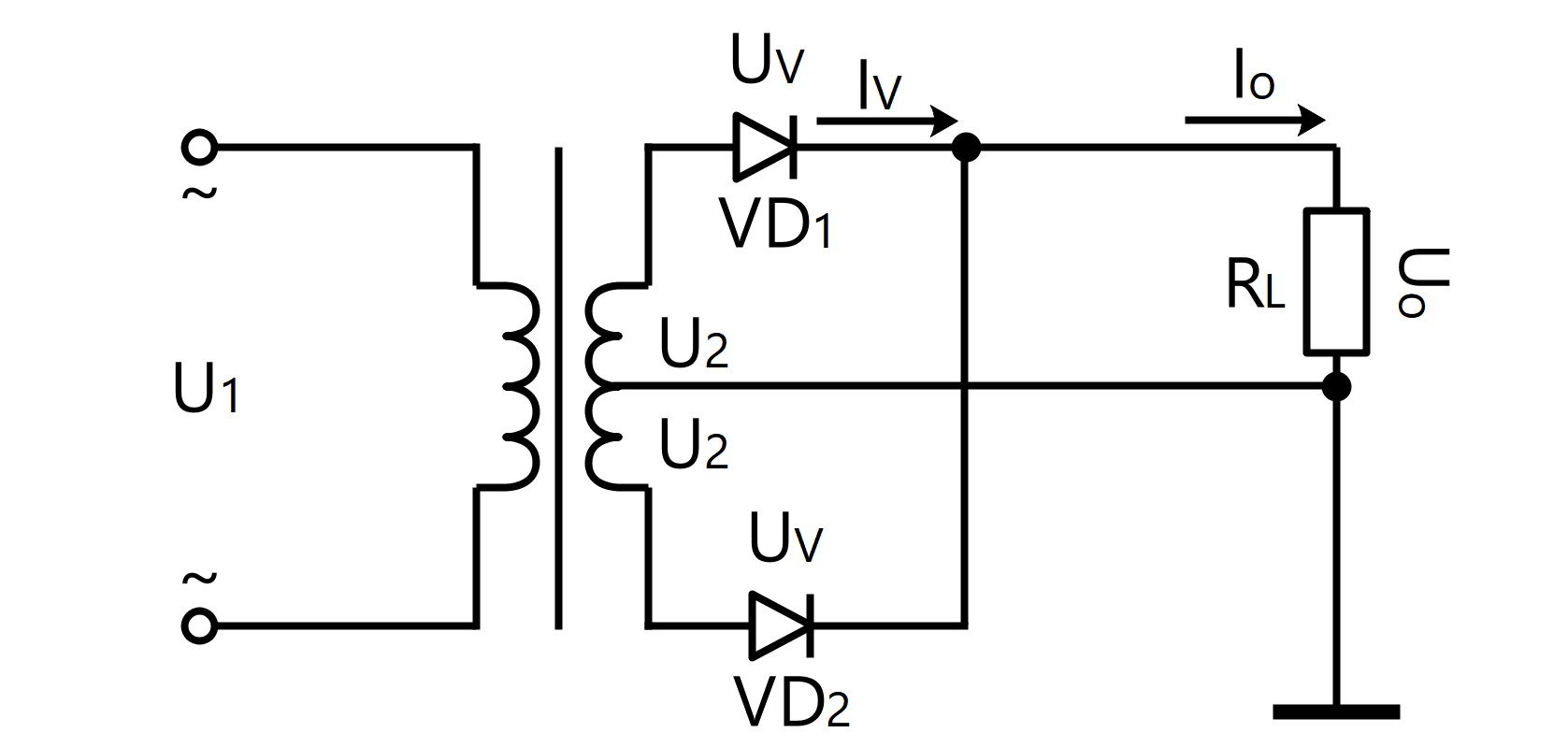
●วงจรการแก้ไขฟูลคลื่นเฟสเดียว
U 0 = 0.9 · U 2
I 0 = 0.9 · U 2 / R L
I V = 1/2 · I 0
U RM = 2 ·√2· U 2
I 0 = 0.9 · U 2 / R L
I V = 1/2 · I 0
U RM = 2 ·√2· U 2
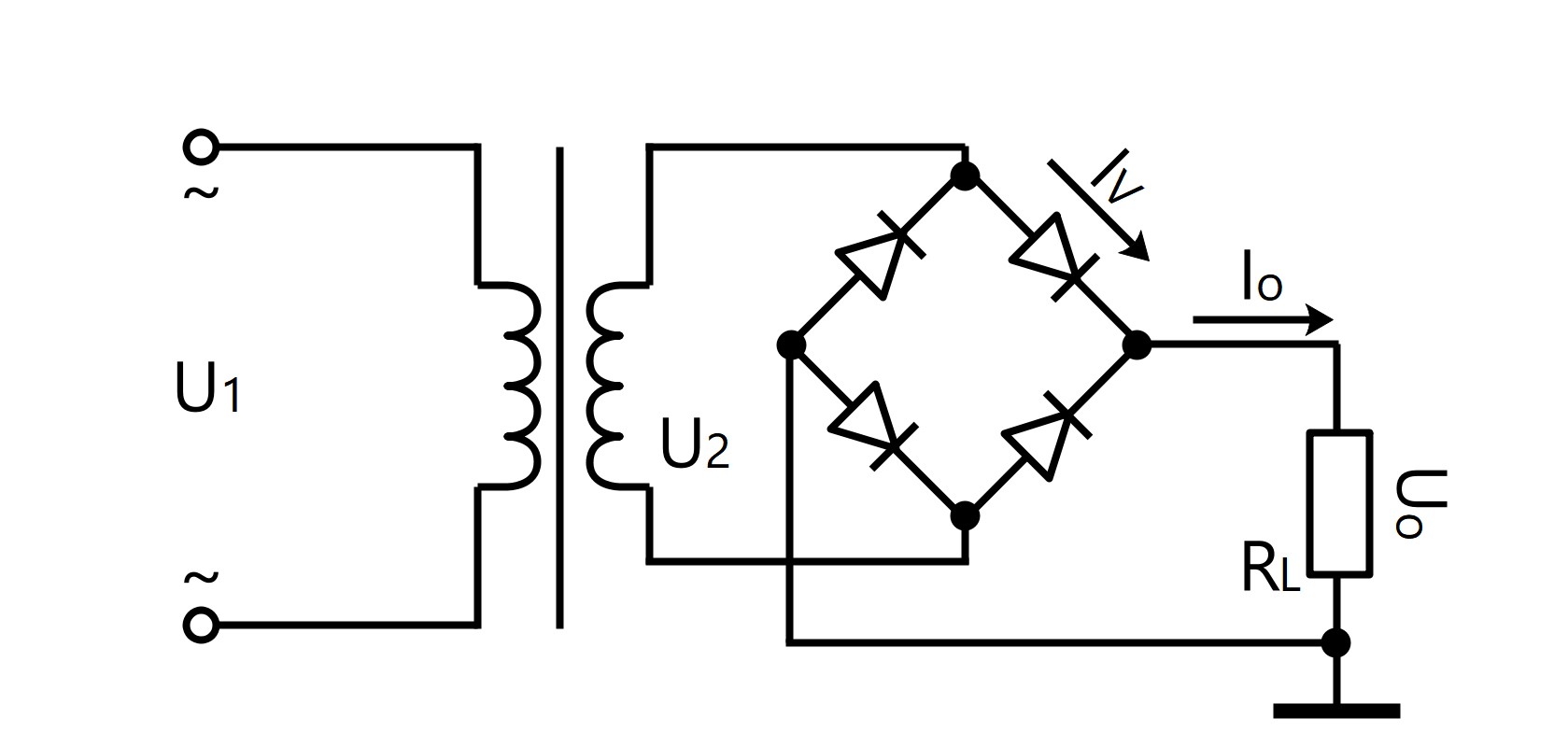
●วงจรการแก้ไขสะพานเฟสเดียว
U 0 = 0.9 · U 2
I 0 = 0.9 · U 2 / R L
I V = 1/2 · I 0
U RM = √2· U 2
I 0 = 0.9 · U 2 / R L
I V = 1/2 · I 0
U RM = √2· U 2
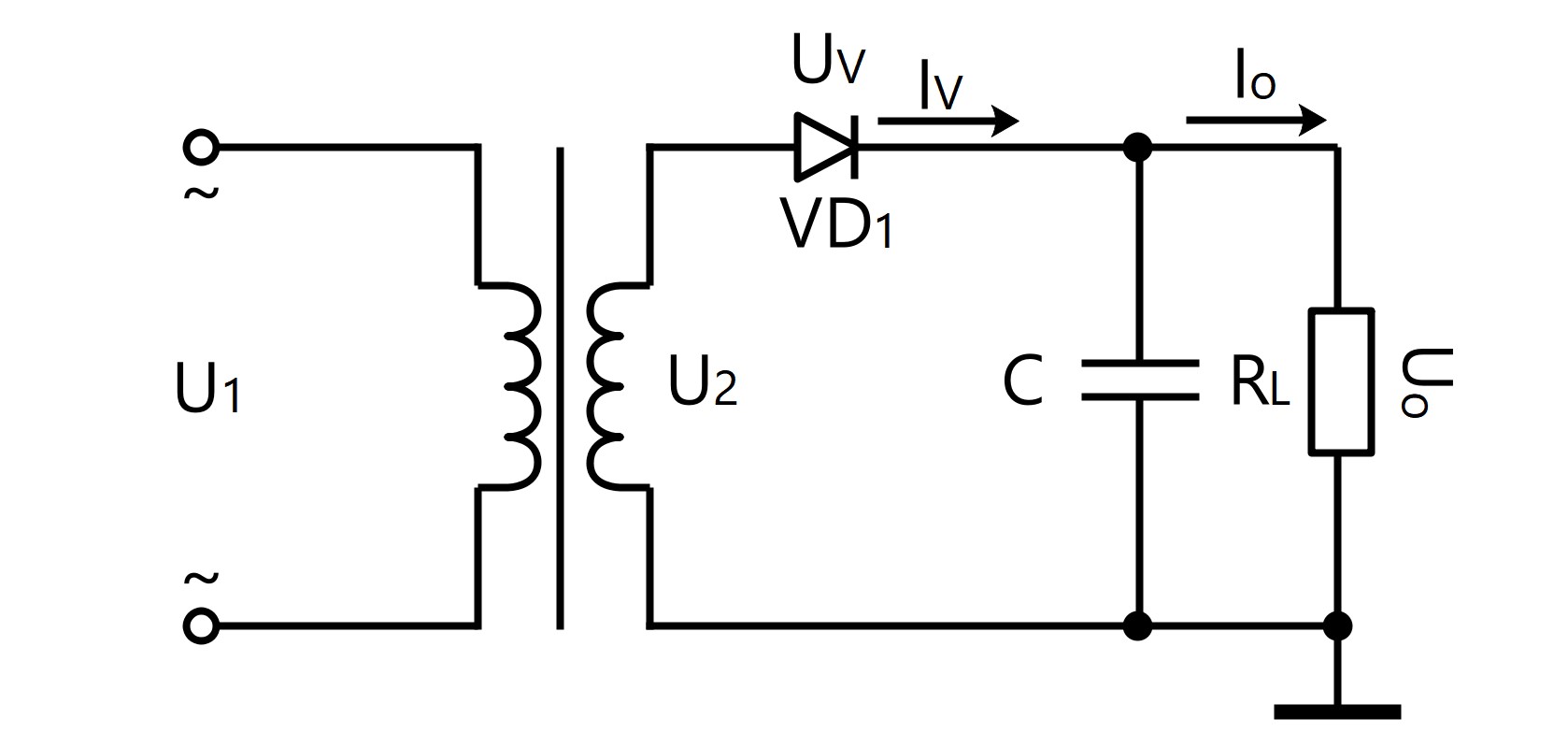
●วงจรฟิลเตอร์แก้ไขการแยกตัวครึ่งคลื่น●เฟสเดียว
U 0 = U 2
I 0 = U 2 / R L
I v = 1/2 · I 0
U RM = 2 ·√2· U 2
C≥ (3 ~ 5) · T / R L
T = 1 / f, ถ้า f = 50Hz แล้ว T = 1/50 = 20ms
I 0 = U 2 / R L
I v = 1/2 · I 0
U RM = 2 ·√2· U 2
C≥ (3 ~ 5) · T / R L
T = 1 / f, ถ้า f = 50Hz แล้ว T = 1/50 = 20ms
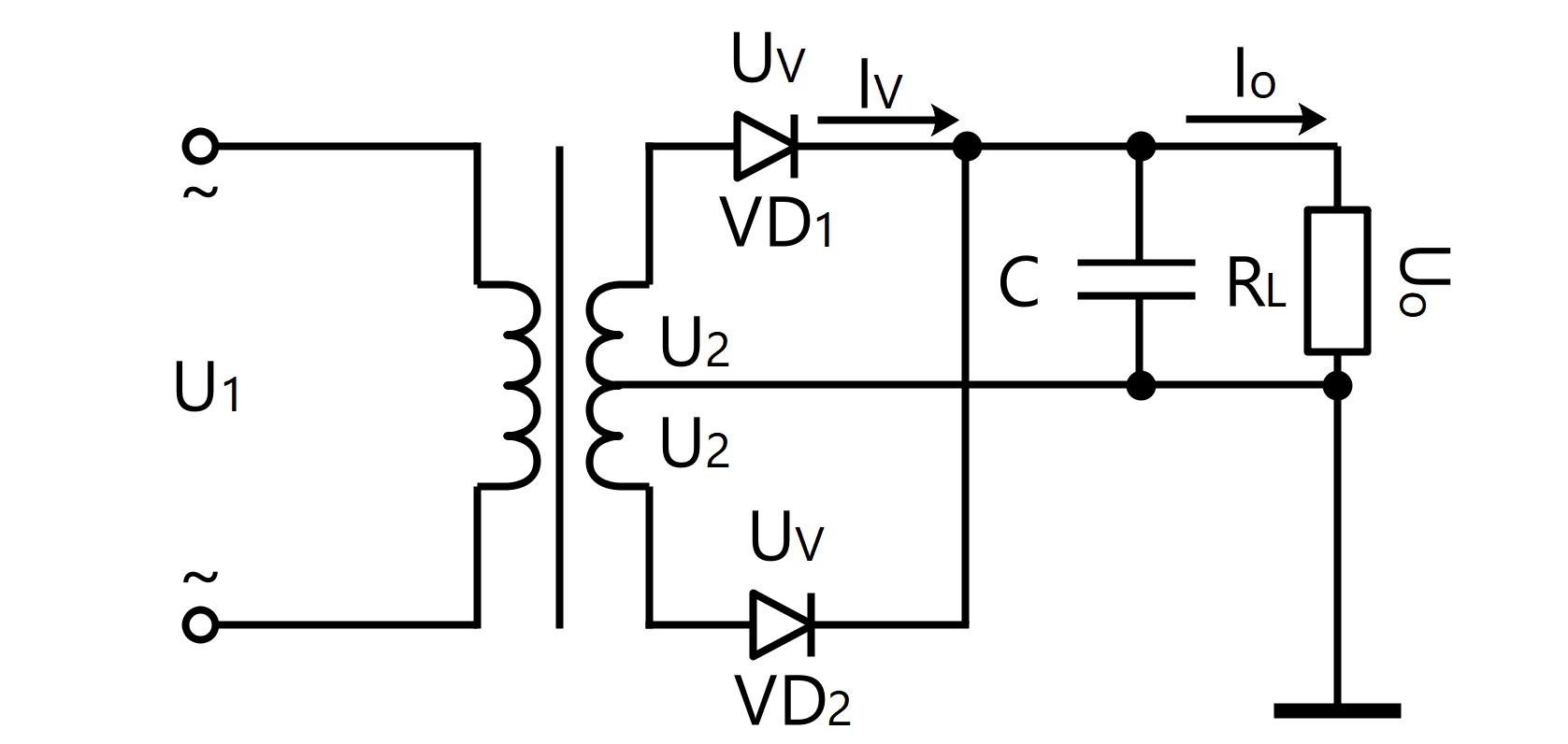
●วงจรกรองการแก้ไขฟูลคลื่นเฟสเดียว
U 0 = 1.2 · U 2
I 0 = 1.2 · U 2 / R L
I v = 1/2 · I 0
U RM = √2· U 2
C≥ (3 ~ 5) · T / 2R L
T = 1 / f ถ้า f = 50Hz ดังนั้น T = 1/50 = 20ms
I 0 = 1.2 · U 2 / R L
I v = 1/2 · I 0
U RM = √2· U 2
C≥ (3 ~ 5) · T / 2R L
T = 1 / f ถ้า f = 50Hz ดังนั้น T = 1/50 = 20ms
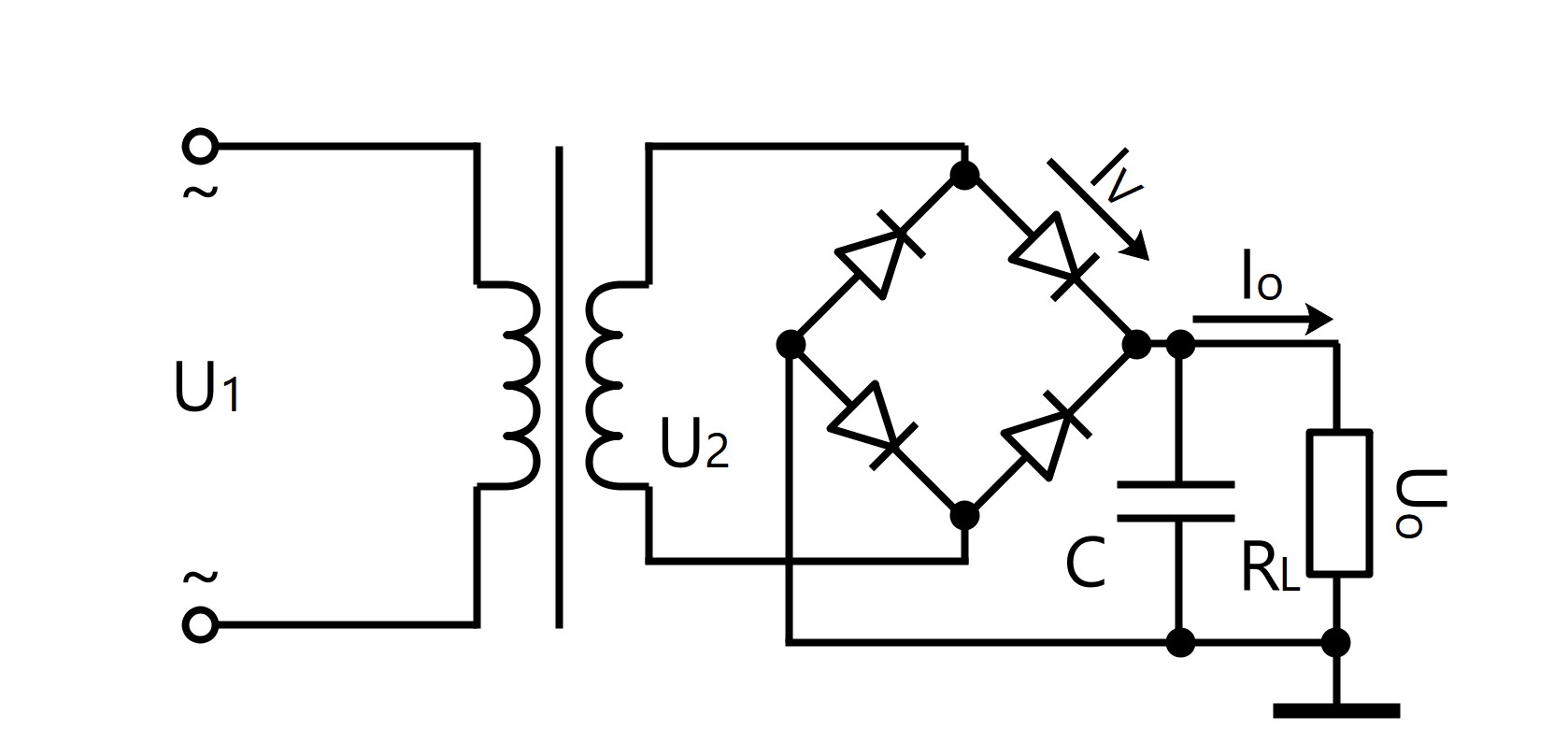
●วงจรกรองการแก้ไขสะพานเฟสเดียว
U 0 = 1.2 · U 2
I 0 = 1.2 · U 2 / R L
I v = 1/2 · I 0
U RM = √2· U 2
C≥ (3 ~ 5) · T / 2R L
T = 1 / f ถ้า f = 50Hz ดังนั้น T = 1/50 = 20ms
I 0 = 1.2 · U 2 / R L
I v = 1/2 · I 0
U RM = √2· U 2
C≥ (3 ~ 5) · T / 2R L
T = 1 / f ถ้า f = 50Hz ดังนั้น T = 1/50 = 20ms
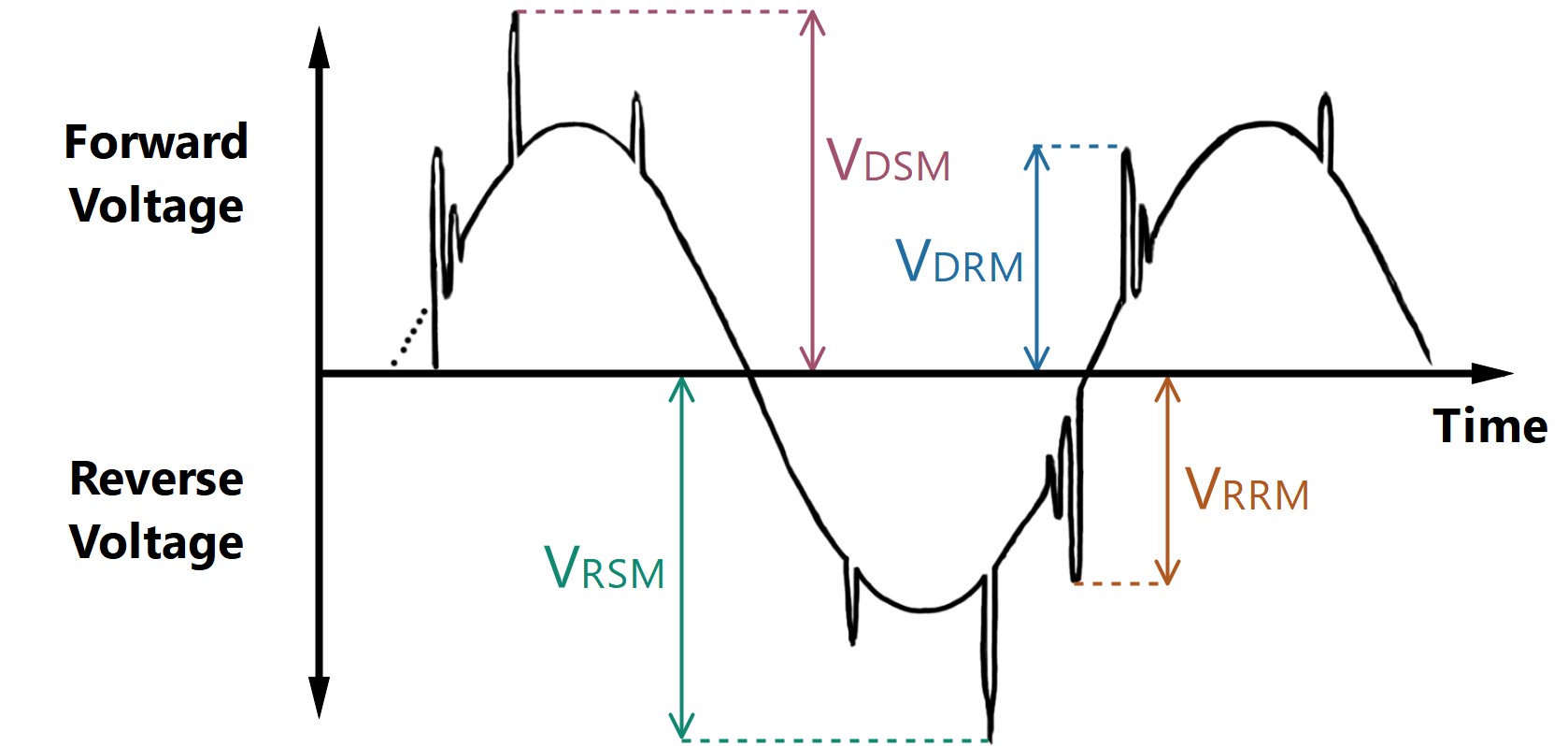
V RSM = V RRM + 200V
V RSM (แรงดันย้อนกลับสูงสุดแบบไม่ทำซ้ำ) เป็นค่าแรงดันย้อนกลับสูงสุดที่อนุญาตของแรงดันย้อนกลับที่สามารถใช้กับทิศทางย้อนกลับของอุปกรณ์ V RRM (แรงดันย้อนกลับสูงสุดซ้ำ) เป็นค่าสูงสุดที่อนุญาตของแรงดันย้อนกลับที่สามารถนำไปใช้ซ้ำกับทิศทางย้อนกลับของอุปกรณ์
V RSM (แรงดันย้อนกลับสูงสุดแบบไม่ทำซ้ำ) เป็นค่าแรงดันย้อนกลับสูงสุดที่อนุญาตของแรงดันย้อนกลับที่สามารถใช้กับทิศทางย้อนกลับของอุปกรณ์ V RRM (แรงดันย้อนกลับสูงสุดซ้ำ) เป็นค่าสูงสุดที่อนุญาตของแรงดันย้อนกลับที่สามารถนำไปใช้ซ้ำกับทิศทางย้อนกลับของอุปกรณ์
V DSM = V DRM + 200V
V DSM (แรงดัน Off-State Peak แบบไม่ทำซ้ำ) เป็นค่าสูงสุดของการจ่ายแรงดันไฟฟ้าที่อนุญาตให้ใช้สำหรับแรงดันไฟฟ้านอกสถานะที่สามารถใช้ได้กับทิศทางไปข้างหน้าของอุปกรณ์ V DRM (แรงดันไฟฟ้า Off-State Peak ซ้ำ) เป็นค่าสูงสุดที่อนุญาตของแรงดันไฟฟ้านอกสถานะที่สามารถนำไปใช้ซ้ำกับทิศทางไปข้างหน้าของอุปกรณ์
V DSM (แรงดัน Off-State Peak แบบไม่ทำซ้ำ) เป็นค่าสูงสุดของการจ่ายแรงดันไฟฟ้าที่อนุญาตให้ใช้สำหรับแรงดันไฟฟ้านอกสถานะที่สามารถใช้ได้กับทิศทางไปข้างหน้าของอุปกรณ์ V DRM (แรงดันไฟฟ้า Off-State Peak ซ้ำ) เป็นค่าสูงสุดที่อนุญาตของแรงดันไฟฟ้านอกสถานะที่สามารถนำไปใช้ซ้ำกับทิศทางไปข้างหน้าของอุปกรณ์
I t 2 = I TSM 2 · t w / 2
t wคือช่วงเวลาไซน์ครึ่ง ฉันTSMมันเป็นกระแสไฟกระชากที่ไม่ได้ทำซ้ำสูงสุดในหนึ่งรอบ; ถ้าความถี่คือ 50Hz, I t 2 = 0.005 I TSM 2 (แอมป์2 ·วินาที)
t wคือช่วงเวลาไซน์ครึ่ง ฉันTSMมันเป็นกระแสไฟกระชากที่ไม่ได้ทำซ้ำสูงสุดในหนึ่งรอบ; ถ้าความถี่คือ 50Hz, I t 2 = 0.005 I TSM 2 (แอมป์2 ·วินาที)
สูตรคำนวณการสร้างความร้อน
เมื่อรีเลย์สถานะโซลิดกำลังทำงานวงจรเอาท์พุทจะมีแรงดันไฟฟ้าตกที่ 1 ~ 2V เมื่อโมดูลโซลิดสเตต (หรือโมดูลพลังงาน) กำลังทำงานวงจรเอาท์พุทจะมีแรงดันตกที่ 2 ~ 4V และพลังงานไฟฟ้าที่พวกเขาใช้จะถูกส่งเป็นความร้อนและความร้อนนี้จะเกี่ยวข้องกับกระแสไฟฟ้าที่ใช้งานเท่านั้น โซลิดสเตตรีเลย์มีค่าความร้อน 1.5 วัตต์ต่อแอมป์ (1.5 W / A) และโมดูลโซลิดสเตตมีค่าความร้อน 3.0 วัตต์ต่อแอมป์ (3.0 W / A) ความร้อนที่เกิดจากวงจรสามเฟสคือผลรวมของความร้อนที่เกิดขึ้นในแต่ละเฟส
รีเลย์สถานะของแข็งเดี่ยวหรือ DC: P = 1.5 · I
โมดูลโซลิดสเตตเดี่ยวหรือ DC: P = 3.0 · I
P คือความร้อนที่เกิดจากรีเลย์สถานะของแข็ง / โมดูลโซลิดสเตตและหน่วยเป็น W; ฉันเป็นกระแสไฟฟ้าที่เกิดขึ้นจริงและหน่วยเป็น A
โมดูลโซลิดสเตตเดี่ยวหรือ DC: P = 3.0 · I
P คือความร้อนที่เกิดจากรีเลย์สถานะของแข็ง / โมดูลโซลิดสเตตและหน่วยเป็น W; ฉันเป็นกระแสไฟฟ้าที่เกิดขึ้นจริงและหน่วยเป็น A
โดยปกติถ้ากระแสโหลดเป็น 10A ต้องติดตั้งแผ่นระบายความร้อน หากกระแสโหลดเป็น 40A หรือสูงกว่าต้องติดตั้งชุดระบายความร้อนด้วยอากาศหรือระบายความร้อนด้วยน้ำ
สูตรคำนวณการกระจายความร้อน
ประสิทธิภาพการระบายความร้อนของชุดระบายความร้อนนั้นสัมพันธ์กับวัสดุรูปร่างความแตกต่างของอุณหภูมิและอื่น ๆ
Q = h · A ·η·ΔT
Q คือความร้อนที่กระจายโดยฮีตซิงค์ h คือการนำความร้อนทั้งหมดของชุดระบายความร้อน (W / cm 2 ·° C) โดยทั่วไปวัสดุอลูมิเนียมประมาณ 2.12W / cm 2 ·° C วัสดุทองแดงประมาณ 3.85W / cm 2 ·° C และ วัสดุเหล็กประมาณ 0.46W / cm 2 ° C; A คือพื้นที่ผิวของแผงระบายความร้อน (ซม. 2 ); ηคือประสิทธิภาพของชุดระบายความร้อนซึ่งส่วนใหญ่ถูกกำหนดโดยรูปร่างของชุดระบายความร้อน ΔTคือความแตกต่างระหว่างอุณหภูมิสูงสุดของแผ่นระบายความร้อนและอุณหภูมิโดยรอบ (° C)
Q คือความร้อนที่กระจายโดยฮีตซิงค์ h คือการนำความร้อนทั้งหมดของชุดระบายความร้อน (W / cm 2 ·° C) โดยทั่วไปวัสดุอลูมิเนียมประมาณ 2.12W / cm 2 ·° C วัสดุทองแดงประมาณ 3.85W / cm 2 ·° C และ วัสดุเหล็กประมาณ 0.46W / cm 2 ° C; A คือพื้นที่ผิวของแผงระบายความร้อน (ซม. 2 ); ηคือประสิทธิภาพของชุดระบายความร้อนซึ่งส่วนใหญ่ถูกกำหนดโดยรูปร่างของชุดระบายความร้อน ΔTคือความแตกต่างระหว่างอุณหภูมิสูงสุดของแผ่นระบายความร้อนและอุณหภูมิโดยรอบ (° C)
ดังนั้นสามารถหาได้จากสูตรด้านบนว่าพื้นที่ผิวของฮีตซิงค์มีขนาดใหญ่ขึ้นความแตกต่างจากอุณหภูมิโดยรอบก็ยิ่งมากขึ้นและประสิทธิภาพในการระบายความร้อนก็จะดีขึ้นเท่านั้น
การแปลงหน่วยทั่วไป
1MΩ = 10 3 kΩ = 10 6 Ω = 10 9 mΩ
1F = 10 3 mF = 10 6 μF = 10 9 nF = 10 12 pF
1H = 10 3 mH = 10 6 μH
1MV = 10 3 kV = 10 6 V = 10 9 mV = 10 12 μH
1kA = 10 3 A = 10 6 mA = 10 9 μA
1W = 10 3 mW = 1J / s = 1V · A
1HP = 0.75kW
1kW · h = 10 3 W · h = 10 3 V · A · h = 10 6 V · mA · h = 3.6 · 10 6 J
1cm = 10mm = 0.39in
1cm 2 = 0.16sq ใน
° F = 1.8 ° C + 32
K = ° C + 273.15
1F = 10 3 mF = 10 6 μF = 10 9 nF = 10 12 pF
1H = 10 3 mH = 10 6 μH
1MV = 10 3 kV = 10 6 V = 10 9 mV = 10 12 μH
1kA = 10 3 A = 10 6 mA = 10 9 μA
1W = 10 3 mW = 1J / s = 1V · A
1HP = 0.75kW
1kW · h = 10 3 W · h = 10 3 V · A · h = 10 6 V · mA · h = 3.6 · 10 6 J
1cm = 10mm = 0.39in
1cm 2 = 0.16sq ใน
° F = 1.8 ° C + 32
K = ° C + 273.15
ไม่มีความคิดเห็น:
แสดงความคิดเห็น